Recent Images
Sketch The Phase Lines For The Given Differential Equation
An equilibrium point is a sink if the arrows on both sides point towards the equilibrium point and it is a source if both arrows point away from it. A direction field is a graph made up of lots of tiny little lines each of which approximates the slope of the function in that area.
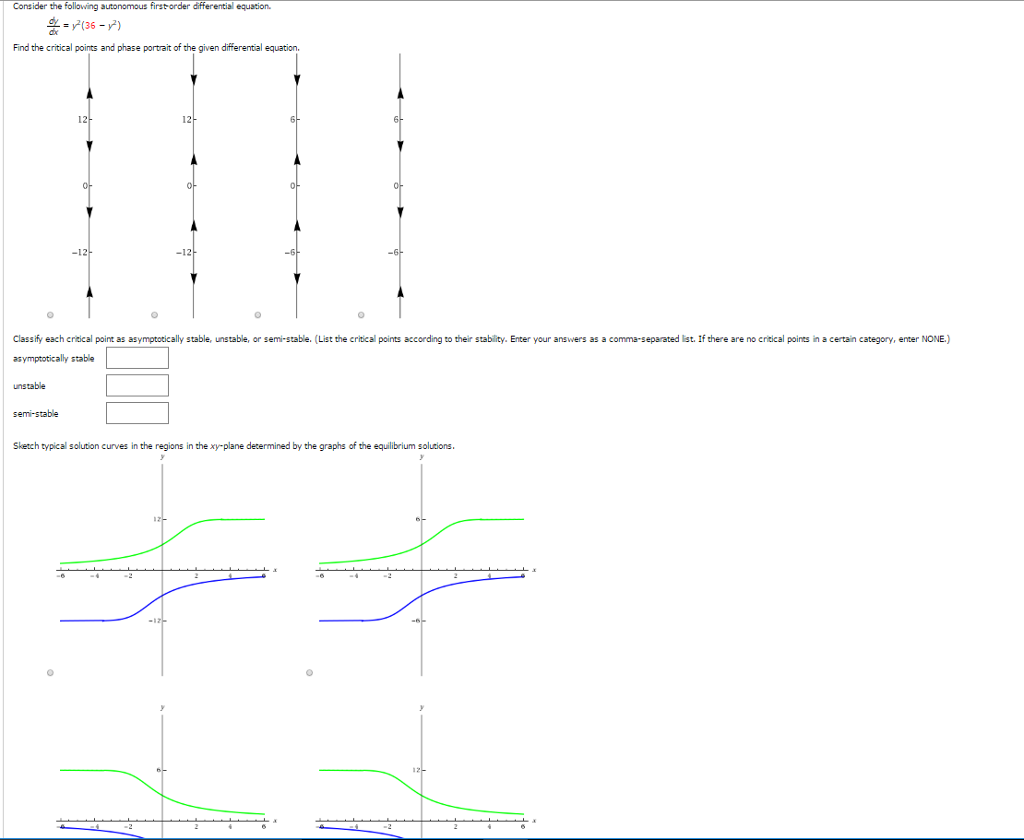
Solved Consider The Following Autonomous First Order Diff
February 7

Solved Problem 2 Asketch The Phase Lines For The Given
You can create a direction field for any differential equation in the form.
Sketch the phase lines for the given differential equation. Where f y 0. Identify the equilibrium points as sinks sources or nodes. Since the direction eld for an autonomous de y f y is constant on horizontal lines its essential content can be conveyed more efciently using the following recipe.
In this context the cartesian plane where the phase portrait resides is called the phase plane. In figure 3 we have sketched the phase line and graph of f for the differential equation. Identify the equilibrium points as sinks sources or nodes.
Identify the equilibrium points as sinks sources or nodes. Sketch the phase lines for the given differential equation. It is quite labor intensive but it is possible to sketch the phase portrait by.
Perhaps the reason for this is our predilection for drawing phase lines vertically so that they line up nicely with the slope field but drawing the y axis horizontally when plotting the graph of f as a function of y. I dydt y 1 sin y ii dydt 3 y3 12y2 b in this problem a differential equation and various initial conditions are specified. How to sketch direction fields.
This will give a vector that represents x at that particular solution. Answer to sketch the phase lines for the given differential equation. The phase line and the graph of the vector field.
As with the single differential equation case this vector will be tangent to the trajectory at that point. I am trying to sketch the phase line and identify equilibrium and i am getting both solutions to be unstable where i think the upper solution has to be stable and the lower one should be unstabl. Sketch the phase lines for the given differential equation.
What is a direction field. Given system of differential equations would behave in the long run. Draw the y axis as a vertical line and mark on it the equilibria ie.
Sketch the graphs of the solution satisfying these initial conditions. We can sketch a bunch of the tangent vectors and then sketch in the trajectories. This vertical line is called the phase line of the equation.
The parametric curves traced by the solutions are sometimes also called their trajectories.
February 7
The Phase Line And The Graph Of The Vector Field

How To Sketch Direction Fields Krista King Math Online
Classification Of Equilibrium Points
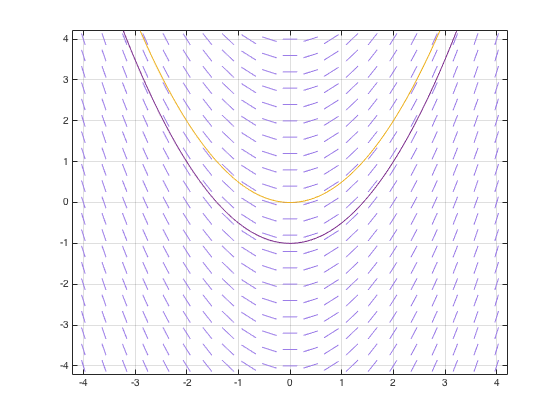
2 Visualizing Solutions To Odes
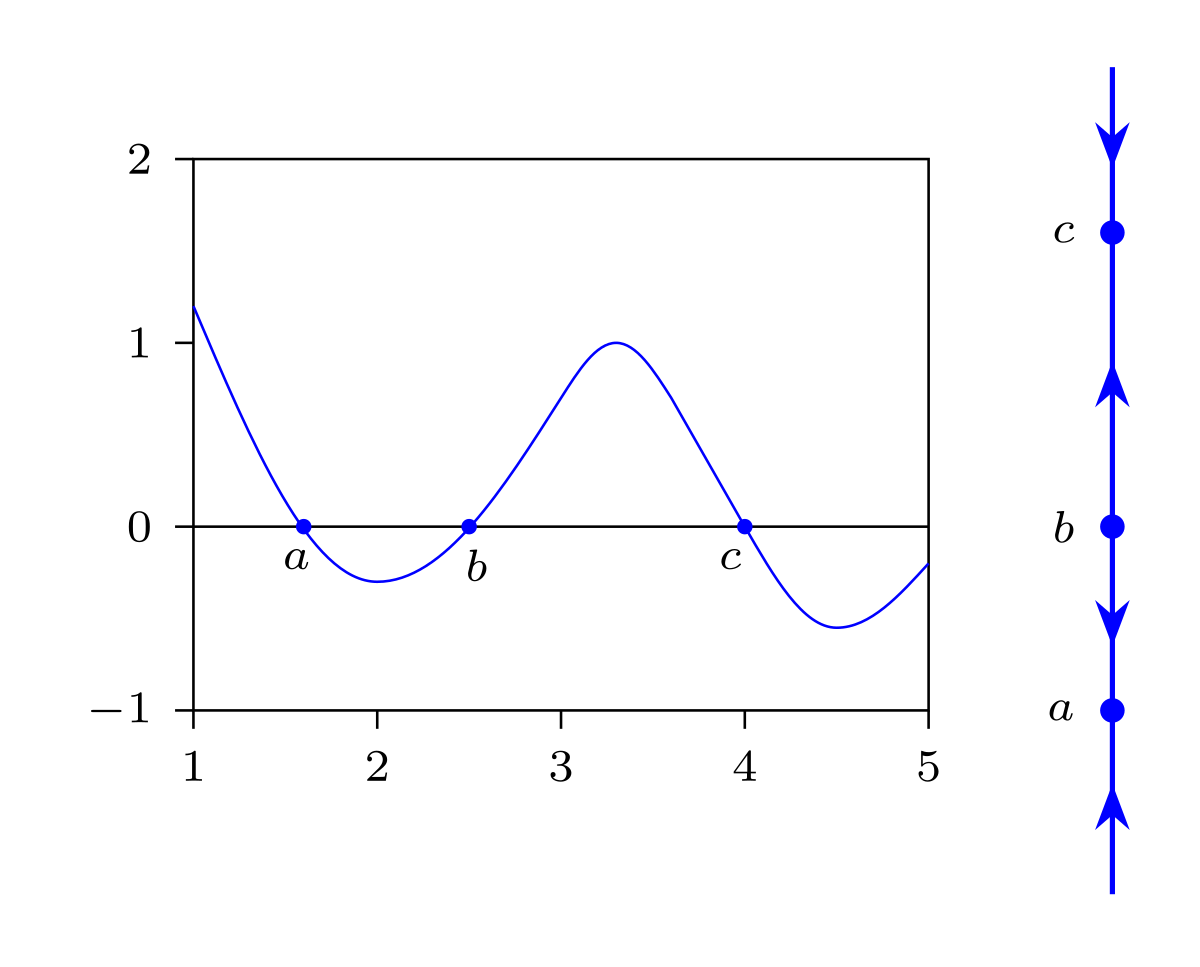
Phase Line Mathematics Wikipedia
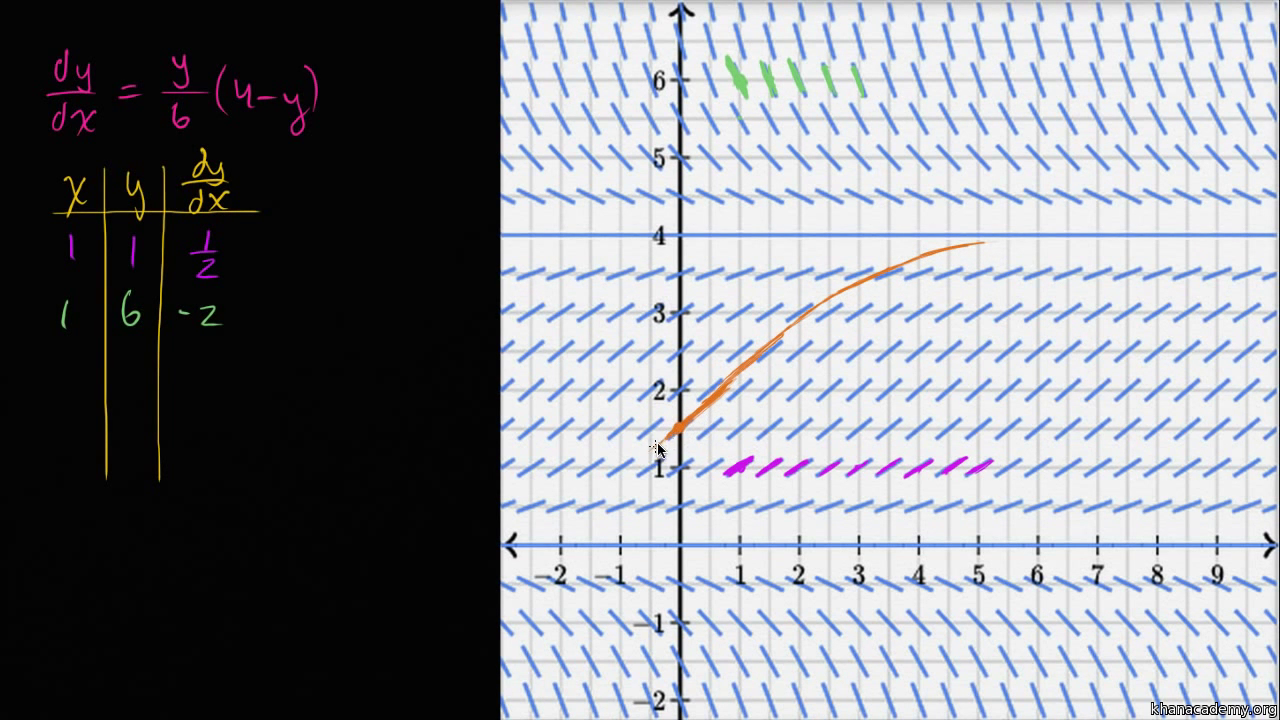
Approximating Solution Curves In Slope Fields
Differential Equations Phase Plane

Differential Equations Introduction Video Khan Academy
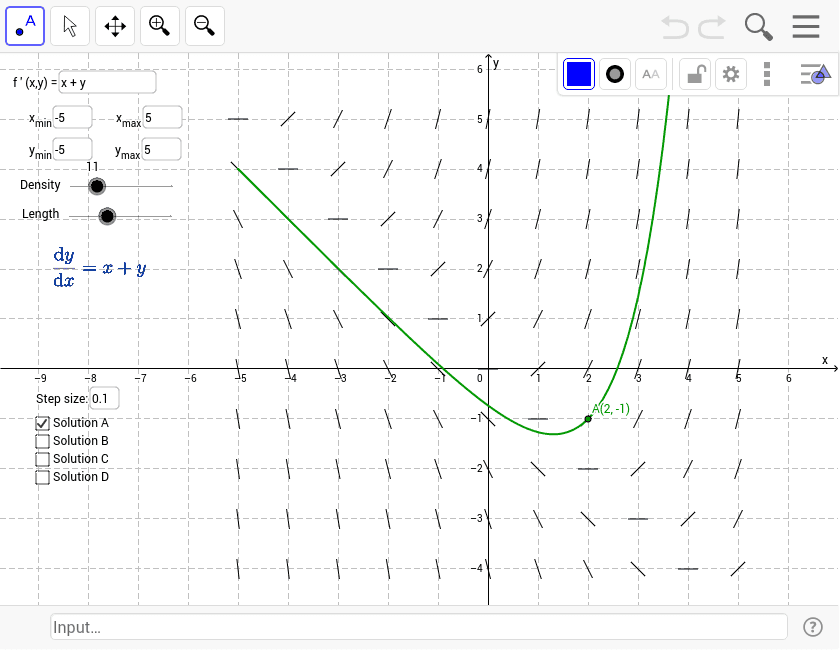
Slope Field Plotter Geogebra
Equilibria And The Phase Line
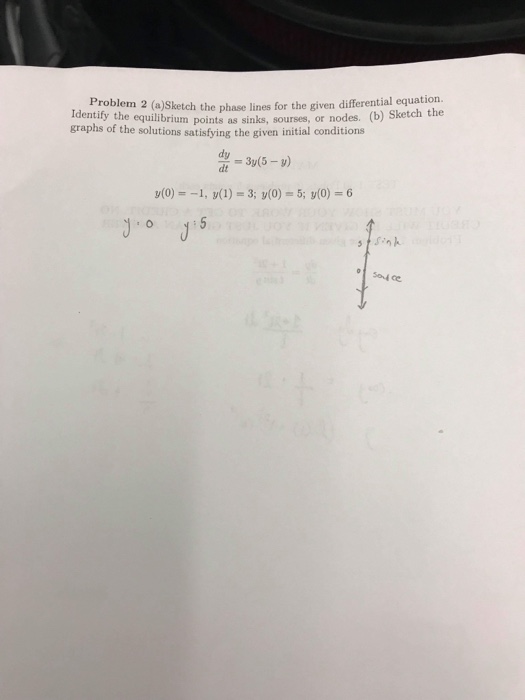
Solved Identfoblem 2 A Sketch The Phase Lines For The G
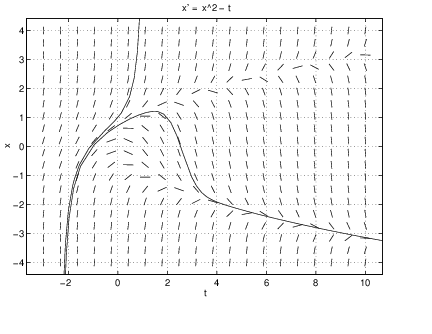
Graphing Solutions To Differential Equations Ximera
Equilibria And The Phase Line

Worked Example Equation From Slope Field Differential
Untitled
Equilibrium Points Of Linear Autonomous Systems
Worked Example Range Of Solution Curve From Slope Field

The Stability Of Equilibria Of A Differential Equation